11 Fully Connected Neural Networks (Scene Classification)
11.1 Topics Covered
- Prepare data for use in a torch/luz workflow
- Create a dataset subclass
- Define a dataloader
- Build an artificial neural network (ANN) architecture by subclass
nn_module() - Use
nn_sequential()to define a model architecture withinnn_module() - Understand the use and parameterization of the following layer types: linear or fully connected (
nn_linear()), batch normalization (nn_batch_norm1d()), and rectified linear unit (ReLU) activation function (nn_relu()) - Fit a model using the luz package
- Implement loss functions and optimizers
- Define callbacks
- Assess a model using withheld data and assessment metrics
11.2 Introduction
We are now ready to start building, training, validating, and using deep learning models. In this chapter, we focus on fully connected architectures using tabulated input data. In the next chapter, we discuss convolutional neural networks using image input data. In both cases, the task of interest is scene classification or scene labeling where the entire sample is predicted to a single class. This is in contrast to semantic segmentation where each pixel is labeled.
In this chapter and the following chapter, we make use of the EuroSat dataset. This dataset is available on GitHub and Kaggle. This paper introduced the data. The version of the dataset used here consists of 27,597 samples labeled to ten categories: annual crop, forest, herbaceous vegetation, highway, industrial, pasture, permanent crop, residential, river, and sea/lake. The input data are 64-by-64 pixel image chips generated from the Sentinel-2 Multispectral Instrument (MSI) sensor, and we use 10 of the 13 bands: blue, green, red, red edge 1, red edge 2, red edge 3, NIR, NIR (narrow), shortwave infrared 1 (SWIR1), and SWIR2. The imagery have a spatial resolution of 10 m, so each chip covers an area of 640-by-640 m. All of the data occur within European countries.
When using a fully connected architecture, each input sample is commonly represented as a row in a table where one column represents the dependent variable and all other columns represent the predictor variables. This means that we cannot use image data in their raw form. There are generally two options for using input image data to train a fully connected architecture: (1) collapse the image into a vector where each element represents a value at a pixel location and for one band or (2) represent the data as summary metrics. When using option 1 and for this dataset, this would result in a very large vector (64 rows X 64 columns X 10 bands = 40,960 values). Also, the spatial structure of the data is not maintained. One option would be to reduce the spatial resolution of the image prior to flattening it to a one-dimensional vector. For our example, we have decided to use option 2: each 64 x 64 pixel chip was aggregated to ten band means. Although this may not be the most optimal way to represent the data, it will suffice for our example.
As normal, we start by reading in the required packages. The tidyverse is used for data wrangling, recipes and yardstick from tidymodels are used for data preprocessing and accuracy assessment, respectively, and torch and luz are used to implement deep learning.
As noted in the prior chapter, you will need access to a CUDA-enabled GPU to execute the code in this chapter.
11.3 Data Preparation
11.3.1 Read and Preprocess
We have already processed the multispectral data to band means and partitioned the data into non-overlapping training, validation, and test sets. We read these CSV files using readr, convert character data to factors, remove the first column, add 1 to the class numeric codes, and shuffle the rows. We have added 1 to the numeric codes since R starts indexing at 1 as opposed to 0. So, contiguous codes from 1 to n, where n is the number of classes, is expected as opposed to 0 to n-1. We shuffle the data to reduced autocorrelation.
It is common to use codes starting at 0 since most languages, including Python, start indexing at 0 instead of 1. It is important to consider this difference in R when preparing your data.
For the training set, we summarize the data to obtain the count of samples per class and the numeric code assigned to each class. The number of samples in each class vary between 1,500 and 2,158. Class imbalance does not appear to be a major issue, so we will not attempt to subsample the data. Class codes are between 1 and 10, as expected.
fldPth <- "gslrData/chpt11/data/"
euroSatTrain <- read_csv(str_glue("{fldPth}train_aggregated.csv")) |>
mutate_if(is.character, as.factor) |>
select(-1) |>
mutate(code = code+1) |>
sample_frac(1, replace=FALSE)
euroSatTest <- read_csv(str_glue("{fldPth}test_aggregated.csv")) |>
mutate_if(is.character, as.factor) |>
select(-1) |>
mutate(code = code+1) |>
sample_frac(1, replace=FALSE)
euroSatVal <- read_csv(str_glue("{fldPth}val_aggregated.csv")) |>
mutate_if(is.character, as.factor) |>
select(-1) |>
mutate(code = code+1) |>
sample_frac(1, replace=FALSE)| class | cnt | code |
|---|---|---|
| AnnualCrop | 1800 | 1 |
| Forest | 1800 | 2 |
| HerbaceousVegetation | 1800 | 3 |
| Highway | 1500 | 4 |
| Industrial | 1500 | 5 |
| Pasture | 1200 | 6 |
| PermanentCrop | 1500 | 7 |
| Residential | 1800 | 8 |
| River | 1500 | 9 |
| SeaLake | 2158 | 10 |
Next, we rescale the band values to a range of 0 to 1 using min-max rescaling. This is accomplished using recipes. Within the recipe() function, we define the formula (class ~ .) and input training data. step_range() is used for the rescaling. The formula is not correct since we do not want to use the numeric code as a predictor variable. However, we are only using this for data preparation and not to train a model in the tidymodels ecosystem, so this is not an issue. All of the predictor variables will be rescaled, other than the class code, to a range of 0 to 1. If a new value falls outside of the range specified by the training data, it will not be clipped. The recipe is prepared using prep() then applied to the training, validation, and test data using bake(). As already noted in the text, data preprocessing should be based on the training data only to avoid a data leak.
myRecipe <- recipe(class ~ ., data = euroSatTrain) |>
step_range(all_numeric_predictors(), -c(code),
min=0,
max=1,
clipping=FALSE)
myRecipePrep <- prep(myRecipe, training=euroSatTrain)11.3.2 Define Dataset Subclass
In the torch environment, a dataset defines how a single sample should be processed while a dataloader defines how mini-batches of samples are fed to the model. A dataset subclass is being defined below for the EuroSat tabulated data. The initialize method defines the inputs or what needs to be generated when an instance of the subclass is instantiated. In this case, the only input is a data frame, which is associated with the variable df. The .getitem method defines how to process a single sample. i represents the row in the table being processed. The predictor variables, columns 2 through 11, are processed to a vector (preds) while the label or dependent variable, column 12, is processed to a separate vector. Both of these vectors are then converted to torch tensors. The predictor variables use a torch_float32() data type while the labels us a torch_int64() (i.e., long integer) data type. squeeze() is used to remove dimensions with a length of one for the label data. Lastly, the predictor variables and label tensors are stored in a list object.
The .length method should return the number of available samples, which is this case is equal to the number of rows in the data frame. As a result, we simply return the number of rows using nrow().
self references the current object or instance. This style of syntax may not be familiar to you if you have not worked with classes. You can think of this as a means to generate properties associated with an object or operations associated with an object (termed methods as opposed to functions) that can operate on the object.
tabDataset <- torch::dataset(
name = "tabDataSet",
initialize = function(df){
self$df <- df
},
.getitem = function(i){
preds <- self$df[i, 2:11] |>
unlist() |>
as.vector() |>
unname()
label <- self$df[i, 12] |>
unlist() |>
as.numeric() |>
as.vector() |>
unname()
predsT <- preds |>
torch_tensor(dtype=torch_float32())
labelT <- label |>
torch_tensor(dtype=torch_int64())
labelT <- labelT$squeeze()
return(list(preds = predsT, label = labelT))
},
.length = function(){
return(nrow(self$df))
}
)11.3.3 Create Datasets and Dataloaders
Once a subclass is defined, it can be used to generate datasets. In the first code block below, we defined training, validation, and test datasets. Next, we define dataloaders for each of the three datasets. We use a mini-batch size of 120. This means that 120 samples will be provided to the model at each iteration or mini-batch, and model parameter updates will be performed after each of the training mini-batches are predicted. The training data are shuffled between epochs to further increase variability. This is not necessary for the validation or test data. Lastly, we drop the last mini-batch for the training and validation dataloaders since they may have a different length than the other mini-batches. The test dataloader uses all samples so that all predictions can be compared to the correct labels to generate assessment metrics.
trainDS <- tabDataset(trainProcessed)
valDS <- tabDataset(valProcessed)
testDS <- tabDataset(testProcessed) trainDL <- torch::dataloader(trainDS,
batch_size=120,
shuffle=TRUE,
drop_last = TRUE)
valDL <- torch::dataloader(valDS,
batch_size=120,
shuffle=FALSE,
drop_last = TRUE)
testDL <- torch::dataloader(testDS,
batch_size=120,
shuffle=FALSE,
drop_last = FALSE)Before moving on, it would be good to check a mini-batch of data. This is accomplished for the training set using .iter() and .next(), which extracts out the first mini-batch. We then print the shapes and data types for the predictor variables and label tensors. The shape for the predictors is [120,10]: 120 samples of 10 predictor variables or band means. The shape for the labels is [120]: 120 numeric class codes. The data type for the predictor variables is float while the labels are stored as a long integer, which is as anticipated. We also obtain the mean, maximum, and minimum band values, which confirm that the data are generally scaled between 0 and 1. In short, the data look to be correctly formatted.
batch1 <- trainDL$.iter()$.next()
batch1$preds$shape[1] 120 10batch1$label$shape[1] 120batch1$preds$dtypetorch_Floatbatch1$label$dtypetorch_Longtorch_mean(batch1$preds, dim=1)torch_tensor
0.2833
0.2965
0.2186
0.2865
0.4621
0.4324
0.4456
0.3033
0.3115
0.4470
[ CPUFloatType{10} ]torch_amax(batch1$preds, dim=1)torch_tensor
0.6740
0.7003
0.6646
0.6642
0.7999
0.7467
0.7676
0.8894
0.8861
0.7795
[ CPUFloatType{10} ]torch_amin(batch1$preds, dim=1)torch_tensor
0.01 *
2.0882
1.9514
0.5343
0.6368
0.4956
0.3971
0.4497
0.6446
0.3429
0.6892
[ CPUFloatType{10} ]11.4 Define Fully Connected Architecture
We are now ready to define a model. Specifically, we will build the model conceptualized in Figure 11.1. The model should accept an input tensor of shape [mini-batch size, 10], since there are 10 image bands or predictor variables, and generate a tensor of shape [mini-batch size, 10], since there are 10 classes being differentiated. A fully connected architecture expects all inputs or outputs from the prior layer to be connected to every node in the current layer, as a result:
- Layer 1 contains 32 nodes, which are each connected to all 10 input values
- Layer 2 contains 64 nodes, which are each connected to the 32 outputs from Layer 1
- Layer 3 contains 128 nodes, which are each connected to the 64 outputs from Layer 2
- Layer 4 has 10 neurons representing each predicted class, which are each connected to the 128 neurons from Layer 3
The first three layers consist of three operations: a linear layer, batch normalization, and rectified linear unit (ReLU) activation. Using torch, fully connected layers are implemented with nn_linear(). 1D batch normalization is implemented with nn_batchnorm1d(), and ReLU is implemented with nn_relu(). The last layer does not incorporate batch normalization or an activation function since its is meant to generate raw logits, which only requires a linear or fully connected layer. If we wanted to convert the raw logits to estimated class probabilities (i.e., rescaled logits), we could include a softmax activation using nn_softmax(); however, that is not necessary here.
For a binary classification, the last layer could have two nodes or neurons or just one. If two nodes are used, then one node will generate a logit for the positive case while the other will generate a logit for the negative or background case. These could then be rescaled to sum to one using a softmax activation. If only one node is used, then only the logit for the positive case is generated. This can then be rescaled using a sigmoid activation (nn_sigmoid()). In short, there are different means to define a binary classification problem. How the problem is defined can impact the architecture requirements, required rescaling method, applicable loss functions, and accuracy assessment metric interpretation.
For a multiclass problem, the number of neurons in the last layer must be equal to the number of classes being differentiated.

Before generating the model architecture, let’s also discuss the number of trainable parameters. For a fully connected layer, the number of trainable weights is equal to the number of inputs multiplied by the number of outputs. There is also a bias parameter associated with each neuron. For the first layer, this means that there will be a total of 320 weights (10 X 32) and 32 biases. 1D batch normalization has shift and scale parameters for each neuron; as a result, for the first layer, the total number of center and scale parameters is 64. ReLU activation has no trainable parameters. Make sure to spend some with Figure 11.1 to make sure you understand the number of trainable parameters per layer.
Using torch, a model architecture is defined by subclassing nn_module(). The initialize() method instantiates the parameters provided to the model and also its components. Our model has three user-defined inputs. inFeat is the number of input predictor variables, nNodes is a vector of the number of nodes or neurons for the first three layers, and nCls is the number of classes being differentiated, which defines the number of neurons in the final layer.
The networks architecture is defined using nn_sequential(). This allows you to define a series of operations that, as the name implies, happen sequentially. This can be used in this case since there is only one “path” through the network: all data must pass through all layers in the model. In later chapters, we work with models that are not fully sequential, for example those that include residual connections or skip connections. In such cases, the entire model cannot be defined within one call to nn_sequential(). The first three layers conceptualized in Figure 11.1 are implemented using nn_linear(), nn_batch_norm1d(), and nn_relu(). The last layer only requires nn_linear(). Make sure you understand how this is implemented within nn_sequential(). For nn_linear(), the first argument denotes the number of inputs while the second argument denotes the number of outputs or nodes in the layer. For nn_batch_norm1d(), the single argument is the number of nodes from the prior linear layer. There are no required arguments for nn_relu(), and it has no trainable parameters.
The forward() method defines how data propagate through the model. In our case, the forward() method is very simple: the data, x, are passed through self$net() and the result is returned.
myANN <- torch::nn_module(
"ANN",
initialize = function(inFeat=10,
nNodes=c(32,64,128),
nCls) {
self$inFeat = inFeat
self$nNodes = nNodes
self$nCls = nCls
self$net <- nn_sequential(
nn_linear(inFeat, nNodes[1]),
nn_batch_norm1d(nNodes[1]),
nn_relu(),
nn_linear(nNodes[1], nNodes[2]),
nn_batch_norm1d(nNodes[2]),
nn_relu(),
nn_linear(nNodes[2], nNodes[3]),
nn_batch_norm1d(nNodes[3]),
nn_relu(),
nn_linear(nNodes[3], nCls)
)
},
forward = function(x) {
x <- self$net(x)
return(x)
}
)Executing the above code creates the subclass. To actually instantiate an instance of the subclass requires using the defined subclass. This is accomplished in the next code block were we first instantiate the instance with our required arguments and save it to the variable model. We then test the model by passing some random data with the correct shape through it. The data are generated using torch_rand() with a shape of [4,10]: 4 samples each with 10 predictor variables. Printing the result, we confirm that 10 logits are generated, one for each predicted class, for each of the 10 samples. Since the model has not been trained yet but has just been initialized using random parameters, the predictions are meaningless. Here, we are only interested in whether the output shape is correct.
model <- myANN(inFeat=10,
nNodes=c(32,64,128),
nCls=10)
testT <- torch_rand(4, 10)
testTPred <- model(testT)
testTPredtorch_tensor
-0.6531 0.1341 -0.3257 -0.9991 0.2077 -0.4232 0.2979 0.6625 -0.2284 -0.2615
0.3628 0.1281 0.3649 -0.3091 0.2467 -0.3546 0.3604 0.1525 0.3213 0.1504
-0.7825 0.6366 0.3385 0.2650 0.6548 -0.1143 0.0889 -0.5444 -0.0201 -0.6164
0.1184 0.0041 -0.3944 -0.2143 0.5184 -0.3546 -0.2809 -0.0169 -0.0200 0.2421
[ CPUFloatType{4,10} ][ grad_fn = <AddmmBackward0> ]Before training the model, we can get a count of the number of trainable parameters in the model using a custom function, which is defined and used in the code block below. This model has a total of 12,522 trainable parameters. Looking back at Figure 11.1 and by summarizing the trainable parameter counts, we confirm that the total matches the conceptualized architecture.
count_trainable_params <- function(model) {
if (!inherits(model, "nn_module")) {
stop("The input must be a torch nn_module.")
}
params <- model$parameters
trainable_params <- lapply(params, function(param) {
if (param$requires_grad) {
as.numeric(prod(param$size()))
} else {
0
}
})
total_trainable_params <- sum(unlist(trainable_params))
return(total_trainable_params)
}
count_trainable_params(model)[1] 1252211.5 Fit Model with luz
We are now ready to train the model. This could be done by building a training loop from scratch. However, this process is error prone and can be complex depending on the components included in the training process. If you are interested in learning how to implement a custom training loop, we recommend Chapter 14 of Deep Learning and Scientific Computing with R torch.
To simplify the training process, we will use the luz package. The training process is defined using luz in the code block below. We now explain this code in detail since this is a core component of implementing deep learning with the torch ecosystem in R.
-
setup()is used to define the loss function, optimizer, and assessment metrics. In this case, we are using a cross entropy (CE) loss as implemented withnn_cross_entropy_loss(). Note that this loss expects raw logits as opposed to estimated class probabilities. In other words, it implements softmax internally. We are using the AdamW optimizer and calculating overall accuracy usingluz_metric_accuracy()from luz. -
set_hparams()defines the arguments for the network architecture. The provided arguments match those in ourmodelinstance defined above; however, here, we are using the subclass as opposed to an instance of the subclass. In other words, luz will instantiate the model using the settings defined byset_hparams(). -
fit()defines key characteristics of the training process. ThetrainDLdataloader is used to train the model while thevalDLdataloader is used for model validation. The validation data will not be used to train the model or update the model parameters. Instead, they will be predicted at the end of each training epoch to assess for generalization and overfitting issues. The model will be trained for a total of 50 epochs, or passes over the training data. We use two callbacks:luz_callback_csv_logger()will log the training and validation loss and overall accuracy to a CSV file on disk for each epoch whileluz_callback_keep_best_model()will load the the best model after the training process is completed as opposed to just using the model state after the final epoch. As defined, the model state, or set of parameters, after the epoch with the lowest validation loss will be treated as the final model. Lastly, we perform the training on the GPU as opposed to CPU. One very practical benefit of luz is that it can handle moving data and models between devices. This would need to be done manually if using a custom training loop.
If you choose to train the model, note that it will take some time (~15 minute to 45 minutes). We have provided a trained model file if you want to execute the remaining code without training the model.
The final model is saved to disk using luz_save().
fitted <- myANN |>
setup(
loss = nn_cross_entropy_loss(),
optimizer = optim_adamw,
metrics=luz_metric_accuracy()
) |>
set_hparams(
inFeat=10,
nNodes=c(32,64,128),
nCls=10
) |>
fit(data = trainDL,
epochs = 50,
valid_data = valDL,
callbacks = list(luz_callback_csv_logger("gslrData/chpt11/output/annLogs.csv"),
luz_callback_keep_best_model(monitor = "valid_loss",
mode = "min",
min_delta = 0)),
accelerator = accelerator(device_placement = TRUE,
cpu = FALSE,
cuda_index = torch::cuda_current_device()),
verbose=TRUE)
luz_save(fitted, "gslrData/chpt11/output/annModel.pt")11.6 Assess Model
11.6.1 Training Process Results
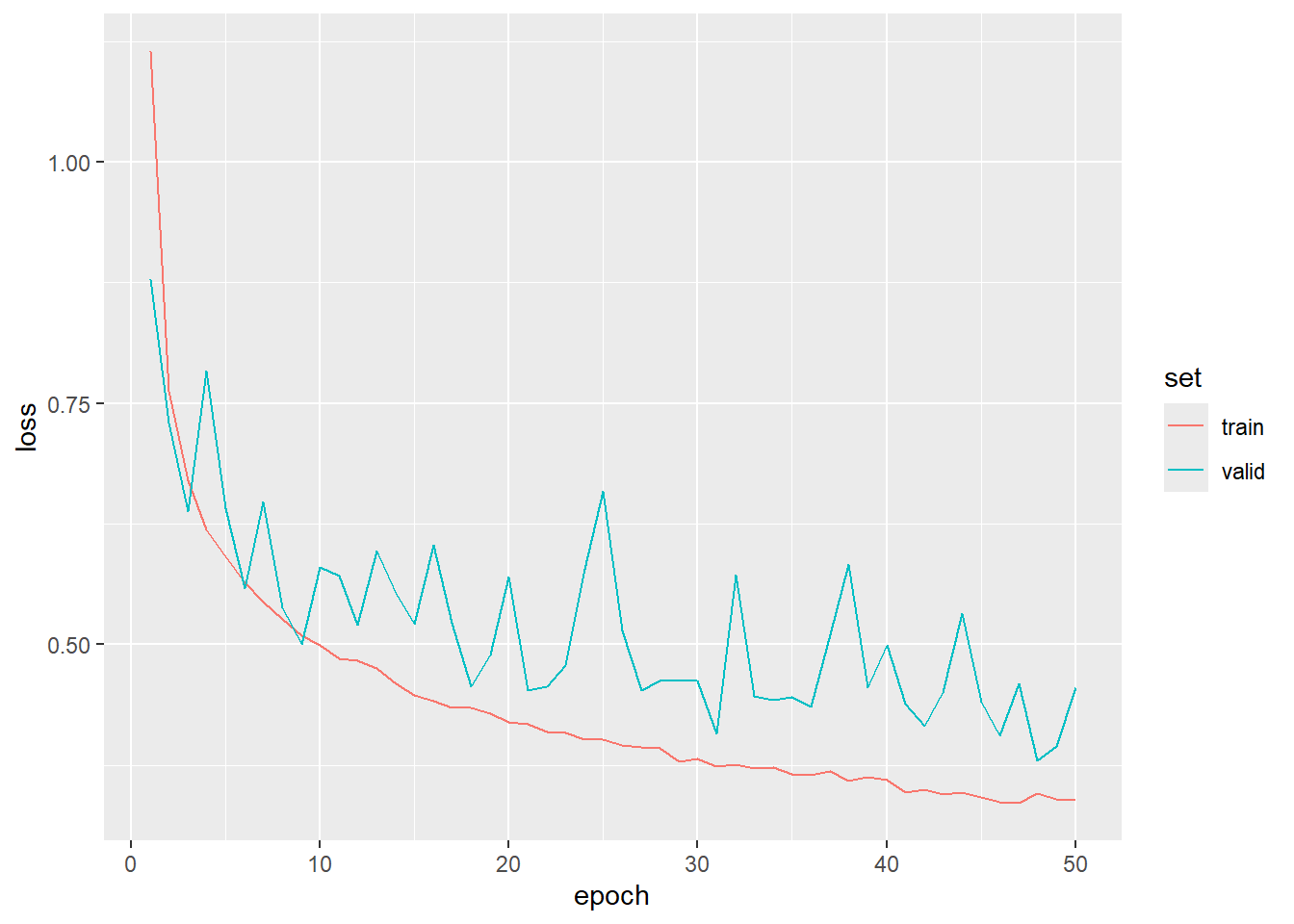
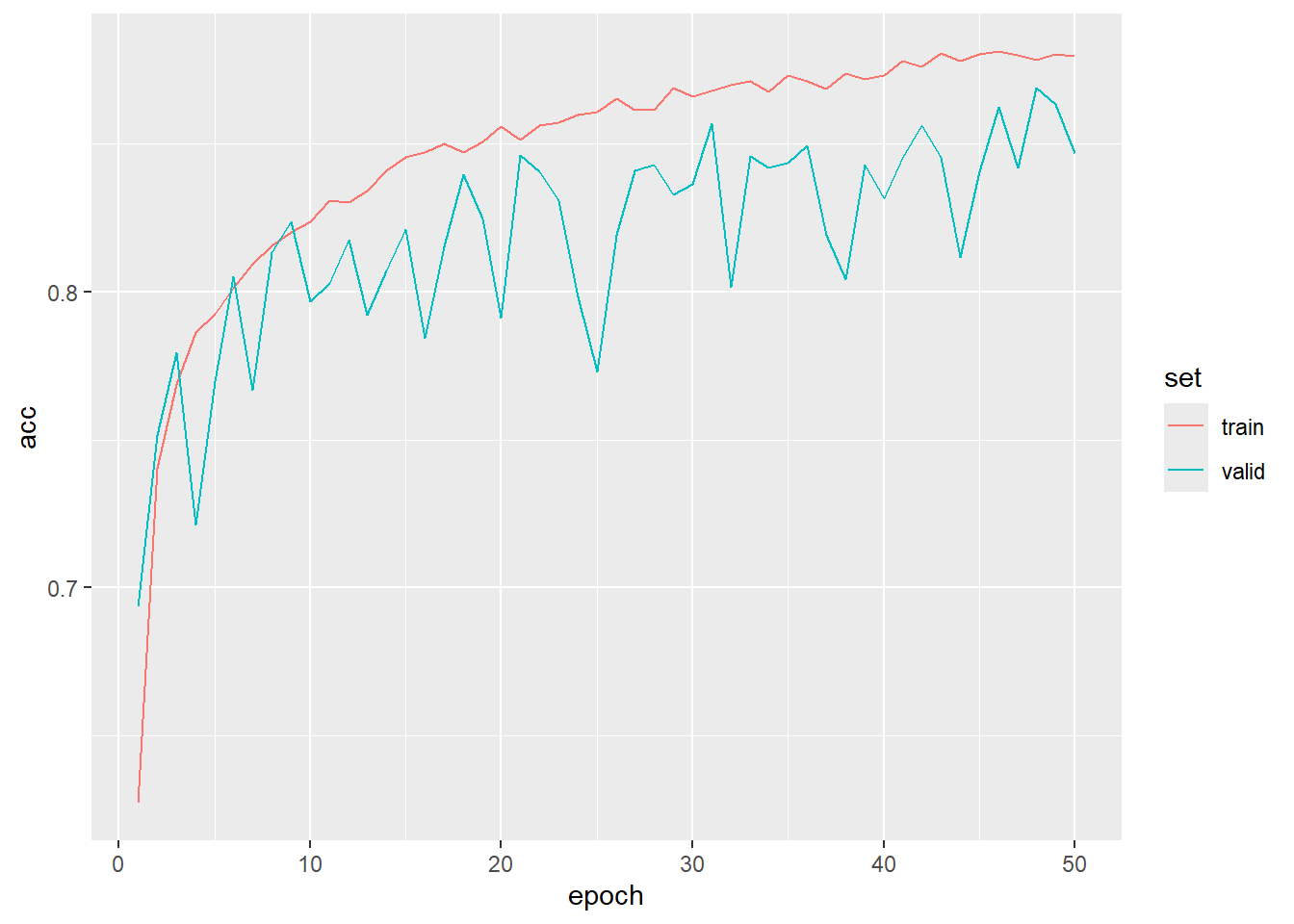
Now that the model is trained, we are ready to assess it. First, we read in the saved log file and print the loss and overall accuracy for both the training and validation data using ggplot(). For the training data, we see a steady decline in the loss and increase in the overall accuracy. However, the largest amount of improvements occurs during the earlier epochs and later improvements are more gradual. The validation loss and overall accuracy is more noisy since these data were not used to update the model parameters. Over the 50 epochs, there was generally not a sign of extreme overfitting; however, the model state after the final epoch was not necessarily the best set of parameters to enhance generalization. Thus, our decision to use luz_callback_keep_best_model() was merited.
logs <- read_csv("gslrData/chpt11/data/annLogs.csv")11.6.2 Predict to Test Data
To further assess the model, we can make predictions to the withheld test set. We first load in the saved model using luz_load(), which accepts a saved model generated by luz_save(). We then use the predict() function to predict the entire test set. The resulting tensor is then moved to the CPU. On the CPU, we extract the vector index that holds the highest logit for each sample using torch_argmax(). This collapses the result from a set of 10 logits for each sample to a single “hard” prediction as a class label. Lastly, the result is converted to an R array.
annModel <- luz_load("gslrData/chpt11/data/annModel.pt")
predTest <- predict(annModel, testDL)$detach()$to(device="cpu")
predTest <- predTest |>
torch_argmax(dim=2) |>
as.array(predTest)11.6.3 Obtain Assessment Metric for Test Data
We now need to build a table that includes both the correct labels and the predictions. We first extract out the correct label from the test set. The predictions are converted to factors then recoded from numeric codes to class names to match the names used in the truth column. The reference data and predictions are then merged to a new data frame.
truth <- euroSatTest$classclasses <- levels(euroSatTest$class)
predTest <- as.factor(predTest) |>
fct_recode("AnnualCrop" = "1",
"Forest" = "2",
"HerbaceousVegetation" = "3",
"Highway" = "4",
"Industrial" = "5",
"Pasture" = "6",
"PermanentCrop" = "7",
"Residential" = "8",
"River" = "9",
"SeaLake" = "10")
resultsDF <- data.frame(truth=truth,
pred=predTest)Using yardstick and the data frame of reference and predicted labels, we next calculate overall accuracy, recall, precision, F1-score, and a confusion matrix. For recall, precision, and F1-score we use macro-averaging so that each class has equal weight in the aggregated metric. If you trained the model on your own and because there is some randomness associated with the model, for example the random weight initiations, you will likely obtain different assessment results than we did. The overall accuracy was 0.869 (86.9%) while the macro-averaged F1-score was 0.858. The confusion between classes highlighted in the confusion matrix generally makes sense. For example, there was some confusion between annual and permanent crop.
We will explore this same classification but using a CNN architecture and the image data as opposed to the aggregated data in the next chapter, and we will compare the CNN results with the results obtained in this chapter.
accuracy(resultsDF,
truth=truth,
estimate=pred)$.estimate[1] 0.8686594recall(resultsDF,
truth=truth,
estimate=pred,
estimator="macro")$.estimate[1] 0.8612556precision(resultsDF,
truth=truth,
estimate=pred,
estimator="macro")$.estimate[1] 0.8575771f_meas(resultsDF,
truth=truth,
estimate=pred,
estimator="macro")$.estimate[1] 0.858103conf_mat(resultsDF,
truth=truth,
estimate=pred) Truth
Prediction AnnualCrop Forest HerbaceousVegetation Highway
AnnualCrop 532 2 11 62
Forest 0 586 1 10
HerbaceousVegetation 12 1 560 24
Highway 19 5 8 238
Industrial 8 0 3 26
Pasture 4 1 3 25
PermanentCrop 19 0 8 32
Residential 4 0 5 62
River 2 5 1 21
SeaLake 0 0 0 0
Truth
Prediction Industrial Pasture PermanentCrop Residential River
AnnualCrop 2 3 11 10 5
Forest 0 0 0 0 10
HerbaceousVegetation 6 3 6 3 15
Highway 23 8 26 35 40
Industrial 444 0 4 24 7
Pasture 0 379 14 1 9
PermanentCrop 1 2 432 12 3
Residential 21 0 6 512 10
River 3 5 1 3 397
SeaLake 0 0 0 0 4
Truth
Prediction SeaLake
AnnualCrop 1
Forest 0
HerbaceousVegetation 0
Highway 0
Industrial 0
Pasture 0
PermanentCrop 0
Residential 0
River 4
SeaLake 715Using the micer package, we can obtain a variety of class-level and aggregated assessment metrics to further explore the results. This is demonstrated in the next code block.
library(micer)
mice(resultsDF$truth,
resultsDF$pred,
mappings=levels(as.factor(resultsDF$truth)),
multiclass = TRUE)$Mappings
[1] "AnnualCrop" "Forest" "HerbaceousVegetation"
[4] "Highway" "Industrial" "Pasture"
[7] "PermanentCrop" "Residential" "River"
[10] "SeaLake"
$confusionMatrix
Reference
Predicted AnnualCrop Forest HerbaceousVegetation Highway
AnnualCrop 532 2 11 62
Forest 0 586 1 10
HerbaceousVegetation 12 1 560 24
Highway 19 5 8 238
Industrial 8 0 3 26
Pasture 4 1 3 25
PermanentCrop 19 0 8 32
Residential 4 0 5 62
River 2 5 1 21
SeaLake 0 0 0 0
Reference
Predicted Industrial Pasture PermanentCrop Residential River
AnnualCrop 2 3 11 10 5
Forest 0 0 0 0 10
HerbaceousVegetation 6 3 6 3 15
Highway 23 8 26 35 40
Industrial 444 0 4 24 7
Pasture 0 379 14 1 9
PermanentCrop 1 2 432 12 3
Residential 21 0 6 512 10
River 3 5 1 3 397
SeaLake 0 0 0 0 4
Reference
Predicted SeaLake
AnnualCrop 1
Forest 0
HerbaceousVegetation 0
Highway 0
Industrial 0
Pasture 0
PermanentCrop 0
Residential 0
River 4
SeaLake 715
$referenceCounts
AnnualCrop Forest HerbaceousVegetation
600 600 600
Highway Industrial Pasture
500 500 400
PermanentCrop Residential River
500 600 500
SeaLake
720
$predictionCounts
AnnualCrop Forest HerbaceousVegetation
639 607 630
Highway Industrial Pasture
402 516 436
PermanentCrop Residential River
509 620 442
SeaLake
719
$overallAccuracy
[1] 0.8686594
$MICE
[1] 0.853682
$usersAccuracies
AnnualCrop Forest HerbaceousVegetation
0.8325508 0.9654036 0.8888889
Highway Industrial Pasture
0.5920398 0.8604651 0.8692660
PermanentCrop Residential River
0.8487230 0.8258064 0.8981900
SeaLake
0.9944367
$CTBICEs
AnnualCrop Forest HerbaceousVegetation
0.8121281 0.9611841 0.8753373
Highway Industrial Pasture
0.5514014 0.8465655 0.8590509
PermanentCrop Residential River
0.8336537 0.8045611 0.8880484
SeaLake
0.9936021
$producersAccuracies
AnnualCrop Forest HerbaceousVegetation
0.8866667 0.9766667 0.9333333
Highway Industrial Pasture
0.4760000 0.8880000 0.9475000
PermanentCrop Residential River
0.8640000 0.8533333 0.7940000
SeaLake
0.9930555
$RTBICEs
AnnualCrop Forest HerbaceousVegetation
0.8728441 0.9738208 0.9252024
Highway Industrial Pasture
0.4238024 0.8768432 0.9433978
PermanentCrop Residential River
0.8504525 0.8354453 0.7734796
SeaLake
0.9920138
$f1Scores
AnnualCrop Forest HerbaceousVegetation
0.8587570 0.9710025 0.9105691
Highway Industrial Pasture
0.5277162 0.8740157 0.9066985
PermanentCrop Residential River
0.8562933 0.8393442 0.8428875
SeaLake
0.9937456
$f1Efficacies
AnnualCrop Forest HerbaceousVegetation
0.8413922 0.9674612 0.8995794
Highway Industrial Pasture
0.4792542 0.8614384 0.8992508
PermanentCrop Residential River
0.8419693 0.8197124 0.8268140
SeaLake
0.9928073
$macroPA
[1] 0.8612555
$macroRTBUCE
[1] 0.8467302
$macroUA
[1] 0.857577
$macroCTBICE
[1] 0.8425533
$macroF1
[1] 0.8594124
$macroF1Efficacy
[1] 0.844636611.7 Concluding Remarks
Using torch and luz, you can now define, train, and validate an ANN architecture for scene classification or scene labeling. In the next chapter, we explore the same task but using a CNN architecture. Fortunately, and as you will see, the workflow is very similar. The primary difference is how the dataset subclass is defined.
11.8 Questions
- Explain the difference between the mini-batch stochastic gradient descent (SGD), SGD with momentum, RMSprop, and adam optimizers.
- Why is it important to include activation functions inside of ANN architectures?
- Explain the difference between a torch dataset and a torch dataloader.
- Within a torch dataset subclass, explain the purpose of the
.getitem()and.length()methods. - A layer in a fully connected architecture contains 64 neurons, which each have 32 inputs. How many weight and bias terms are associated with this layer?
- The layer described in Question 5 is followed by a batch normalization layer. How many shift and scale parameters will this layer include?
- Explain the difference between a class logit and a class probability. How is a logit converted to a probability?
- A binary classification problem can be framed as predicting only the positive case or predicting both the positive and background case. Explain how the choice of framing will impact the structure of the architecture and the choice of loss function.
11.9 Exercises
The goal of this exercise is to compare different model configurations or training processes to the model and training process implemented in this chapter. Us the same data preparation steps as those demonstrated in the Data Preparation section of of the chapter.
Experiment 1
Train the ANN architecture created in the Define Fully Connected Architecture section using the following optimization algorithms: adamw (already trained above), RMSProp, and stochastic gradient descent (SGD). You can use the default settings, including the learning rate, for each optimizer. Train the models for 50 epochs and log the training and validation losses to a CSV file. Use ggplot2 to plot the training losses by epoch using the three different optimizer. Write a paragraph describing the results of the experiment and how the choice of optimization algorithm impacted the rate at which the loss decreased, the final loss obtained, and the difference between the training and validation loss curves.
Experiment 2
Reconfigure the ANN architecture created in the Define Fully Connected Architecture section to not include batch normalization layers. Train the model using the same process as used in the Fit Model with luz section. Save the training and validation losses to disk as a CSV file. Compare the losses by epoch for the original model and the model without batch normalization. Use ggplot2 to plot the training losses by epoch using the two different models. Write a paragraph that describes your results and the impact that including batch normalization layers had on the rate at which the loss decreased, the final loss obtained, and the difference between the training and validation loss curves.
Experiment 3
Train the original model described in the chapter text using the adamw optimizer for 50 epochs using learning rates of 0.0001, 0.001, and 0.01. Log the training and validation losses to disk as a CSV file. Use ggplot2 to plot the training losses by epoch using the three different learning rates. Write a paragraph that describes how the learning rate impacted the rate at which the loss decreased, the final loss obtained, and the difference between the training and validation loss curves.